
Modern prestack amplitude vs. azimuth inversions perform a one-step process to produce both elastic property volumes and a lithology-fluid classification. The Bayesian formulation supplies not just the classification result but also posterior probability volumes for each possible class, thus permitting risking of the interpretation and understanding of ambiguities in the classification. A further benefit of this method is that horizons may be updated by the inversion and uncertainties attached to them, opening the way to risked volumetrics.
As with any inversion, a prior model is required to supply low-frequency information on elastic properties. Traditional methods use elastic property volumes, typically constructed by some form of structurally guided interpolation of well data such as co-kriging. The one-step Bayesian approach differs from this, requiring a prior model for the probabilities of each litho-fluid class at each voxel location, with prior elastic properties derived from the prior probability model. The value of a probabilistic prior lies in the ease with which geological information may be incorporated. For example, one may specify that a brine sand cannot lie directly over a gas sand if these are defined as two distinct litho-fluid classes. Combining such constraints with horizons is a powerful way to construct a detailed prior model suited to a high-resolution inversion in cases where plenty of well information is available, such as a production environment. On the other hand, in exploration settings where wells may be sparse, a relatively simple prior model may still be used effectively to produce informative inversion results.
Two examples are shown illustrating the range of applications. In example A, no well information was used. A single broad litho-class was defined covering the full extent of the rock physics parameter space. A zero-phase statistical wavelet was extracted from the data within the target interval. As in any inversion, some knowledge of the wavelet phase is necessary, and uncertainty in the phase contributes to uncertainty in the position of layer boundaries. Since there was only a single litho-fluid class, the prior model was a constant probability of 1 for that class, and the prior elastic property model had constant values of compressional velocity (Vp), shear velocity (Vs) and density throughout. Since there is no structure in the prior model, and it is only a 0-Hz model, the outcome of the inversion has to be considered as a relative inversion. The figure shows results at a well used as a blind test. In general, the automated interpretation and Vp/Vs curves from the inversion match well within the seismic bandwidth. The strong contrast in both automated interpretation and Vp/Vs at the top reservoir was not recovered, as this would require frequencies outside the seismic range.
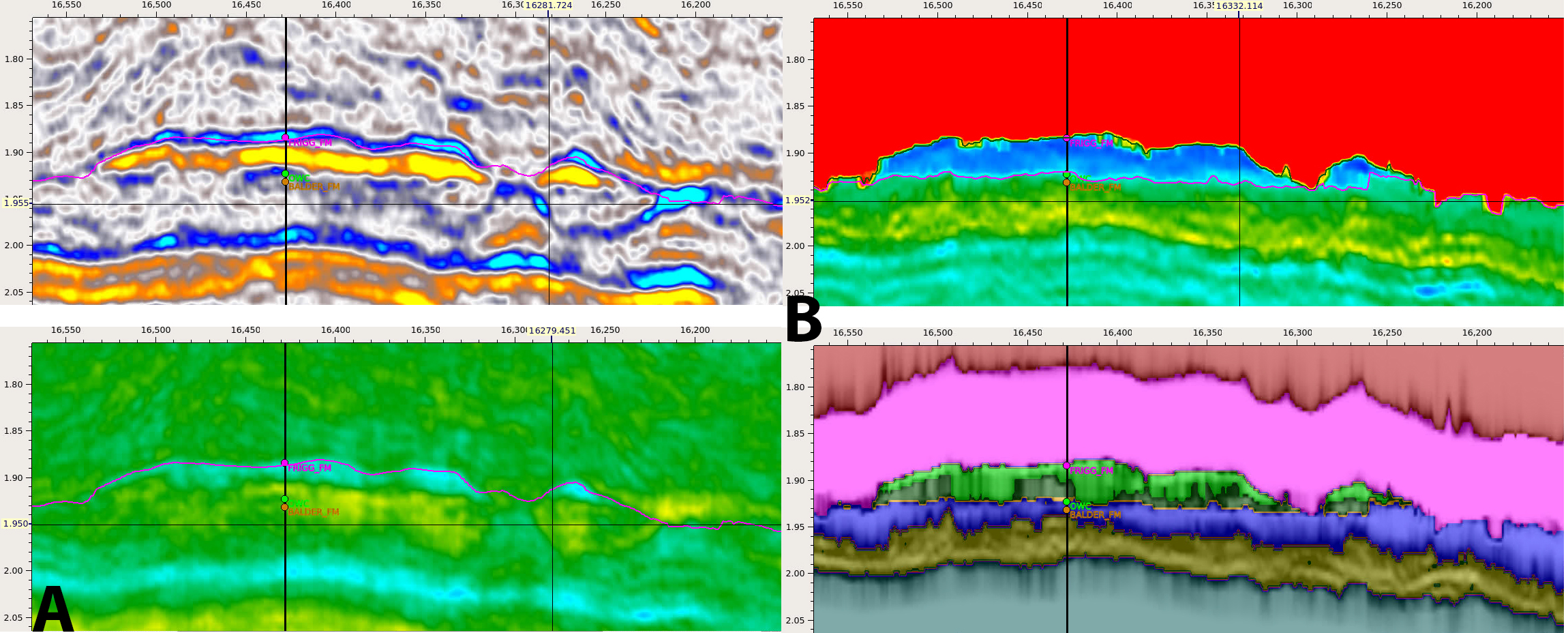
Image A is an example of a prior model with no well information, while Image B shows a prior model more typical of a production setting. (Images courtesy of Sharp Reflections)
Example B used the same data, but this time a detailed prior model was constructed making use of well data and horizons. In this case, there is interest in discriminating between the upper, harder, lower porosity reservoir sand and the lower, softer, higher porosity sand. In addition, the thin cemented zone at the base of the hydrocarbon column would be useful for volumetric studies if it could be mapped as a fluid contact; however, it is below seismic resolution. A prior model was created using horizons for the top reservoir and for the fluid contact, and associated uncertainties permitted them to be moved by the inversion. In addition, litho-fluid classes were defined separately for the upper and lower hydrocarbon sands, the cemented zone and the brine sand immediately below that. With this very detailed model, the inversion produced a very detailed image of the reservoir, successfully mapping the upper and lower sands and the cemented zone, even though the latter was only one seismic sample thick.
These two examples represent two extremes in the level of detail used in the prior model. They show that very high-resolution results may be obtained where there is sufficient reliable prior information available, such as in a production environment, but the same inversion can still give useful information about relative elastic properties even where well data are lacking.
Recommended Reading
Defeating the ‘Four Horsemen’ of Flow Assurance
2024-04-18 - Service companies combine processes and techniques to mitigate the impact of paraffin, asphaltenes, hydrates and scale on production—and keep the cash flowing.
Tech Trends: AI Increasing Data Center Demand for Energy
2024-04-16 - In this month’s Tech Trends, new technologies equipped with artificial intelligence take the forefront, as they assist with safety and seismic fault detection. Also, independent contractor Stena Drilling begins upgrades for their Evolution drillship.
AVEVA: Immersive Tech, Augmented Reality and What’s New in the Cloud
2024-04-15 - Rob McGreevy, AVEVA’s chief product officer, talks about technology advancements that give employees on the job training without any of the risks.
Lift-off: How AI is Boosting Field and Employee Productivity
2024-04-12 - From data extraction to well optimization, the oil and gas industry embraces AI.
AI Poised to Break Out of its Oilfield Niche
2024-04-11 - At the AI in Oil & Gas Conference in Houston, experts talked up the benefits artificial intelligence can provide to the downstream, midstream and upstream sectors, while assuring the audience humans will still run the show.





