MLPs have been a popular structure for the ownership of midstream and certain other energy-related assets. In a sustained low-interest rate environment, investors appreciate the tax-efficient structure and the ability to receive an attractive yield with upside, as distributions increase and the MLP grows.

Sponsors of MLPs can achieve attractive economics due to their general partner (GP) interest in incentive distribution rights (IDRs). Limited partner (LP) investors have accepted the IDR structure because it incentivizes the GP to grow distributions and aligns their interests. GPs only receive increased IDRs as LPs enjoy increased distributions.

However, this IDR structure is complicated and can make traditional securities’ valuation techniques quite difficult. The relative valuation of the GP interest compared to the LP value is dynamic.

The life cycle of an MLP often concludes with a GP-LP simplification transaction (Williams and ONEOK being the latest), which typically resets the tax basis in all of the assets owned by the LP. In order to evaluate the attractiveness of these transactions for each participant, we need to understand the valuation implications of the IDR structure on relative valuations.

IDRs reviewed

When an MLP is formed, a partnership agreement is created which defines the GP-LP relationship and outlines the economic agreement. Typically, the GP starts out with a 2% economic interest in the MLP and the LP begins with 98%, a portion of which is often also retained by the sponsor on a subordinated basis. The partnership agreement specifies a minimum quarterly distribution (MQD) level for the partnership. In addition to its GP interest, the MLP sponsor’s subordinated units act like common LP units as long as the MQD is maintained until they eventually convert into common LP units; typically, after a certain amount of time or upon reaching certain distribution levels for a number of quarters.

The IDRs kick in as the LP distributions reach certain levels, or tiers.

Tier 1 represents LP distributions from the MQD to a certain threshold where Tier 2 begins. For LP distributions from the MQD up to the first threshold, the LP investors get 98% of the distributions and the GP gets its proportionate 2%. When the LP distributions reach specified levels, the GP is entitled to an increasing percentage of the distributions. The tier levels are usually—but not always—set at percentages above the MQD that correspond to the marginal GP IDR percentage at that level.

A typical IDR breakdown would look like the accompanying table. At each tier, the amount the GP receives is not the percentage of what the LPs receive, but rather that percentage of the total. For example, using this table, at a $0.4025 LP distribution, the GP receives $0.0082 (($0.4025 ÷ .98) x .02). Assuming 100 LP units, the total distribution is $41.07 of which the LPs get $40.25 (98%) and the GP gets 82 cents (2%).

The IDR tiers work the same way as income tax brackets. The IDR percentage only applies to the amount over the tier threshold. For example, using the same table, if the LP distribution per unit were 50 cents, people say the IDRs are at the 25% level. This refers to the marginal rate. In actuality, the GP would be entitled to $0.0352 for every LP unit ((($0.4025 ÷ .98) x .02 = $0.0082) + ((($0.4375 - $0.4025) ÷ .85) x .15 = $0.0062) + ((($0.50 - $0.4375) ÷ .75) x .25 = $0.0208) = $0.0352). In this example with 100 LP units, the total distributions paid would be $50 to the LPs and $3.52 to the GP. The GP’s share of the MLP’s total distribution of $53.52 is 6.6%.

The adjoining graphic represents the GP’s share of the total distribution at various LP levels.

Valuation techniques

Valuation of an MLP can be looked at in several ways. Discounted cash flow, public multiples (EV/EBITDA) and distribution yield are common metrics in the industry. If one were to look at the value of the equity in a traditional corporate entity with enterprise value as a starting point, the exercise is fairly simple: Enterprise Value — Net Debt = Equity Value.

In the case of public companies, analysts typically multiply the share price by the number of shares to get equity value. Net debt can then be added to get enterprise value, which can be compared among similar companies.

In the MLP world, “equity” consists of both the LP and GP interests: LP Value + GP Value + Net Debt = Enterprise Value. Issues arise when analysts multiply the number of LP units by the unit price to get the LP value, but struggle translating that into a total equity value that can be used to derive enterprise value so that multiples can be compared among MLPs.

It would seem that there should be a simple mathematical relationship between the LP value and GP value because their share of distributions is already defined by the partnership agreement and the IDR tiers.

However, the actual LP—GP relative valuation is not only dependent on the current share of distributions relative to the IDR tiers, but also the growth rate and ultimate level of such distributions.

For example, consider the example MLP above that is distributing 50 cents per quarter and is in the 25% splits. Assume that the LP units are traded publicly at $10 per unit, implying an LP value of $1,000. If the firm has $1,000 in net debt, what is the enterprise value? Analysis of the extreme range of potential outcomes highlights the difficulty in precisely estimating the enterprise value.

On the low end, assume that the MLP is expected to stay at the 50 cents quarterly distribution level forever with no growth. In that case, the split is relatively easy, the GP is getting 6.6% of the total distributions forever and the LP is getting 93.4%. Therefore, if the LP interest is worth $1,000, the GP interest must be worth $70.70 ($1,000 ÷ .934 x .066). The enterprise value of the MLP is $2,070.70.

Using the same example but assuming that the quarterly LP distribution will rapidly increase to a level that is deep into the 50% splits provides an upper bound. In that scenario, the total share of distributions to the GP will always be less than 50% as shown in the nearby graph, but at very high levels will eventually approach 50%.

Based on this, the GP interest will approach and almost equal the LP interest. Accordingly, in the example above, the max enterprise value for the MLP, at an LP valuation of $1,000, will approach $3,000 (LP + GP + Net Debt).

Of course, this is theoretical, as a valuation for an MLP that is quickly expected to increase distributions well into the top tier of IDRs (distributions of $1.25 per unit or higher) would likely be valued at more than $10 per unit.

However, these examples help to illustrate that for most MLPs, the bounds for LP valuation as a percentage of the total “equity” value can be definitively identified as current LP percentage of total distributions at the high end and 1 minus the highest IDR split on the low end.

Unfortunately, this is a wide range. It also defeats the purpose of using simple trading multiples to compare MLPs when a simple method to derive enterprise value from LP unit trading levels isn’t possible.

Common simplistic methodology

Many research analysts often simply gross up the LP value by the percentage of distributions going to the LP at that point in time. As shown above, this underestimates the MLP’s enterprise value because it overestimates the LPs share of total “equity” value.

However, for MLPs with similar growth expectations and currently at similar IDR levels, this methodology is better than nothing.

Yield methodology

One way to look at MLP valuations without the issues highlighted above is to avoid looking at enterprise value at all and instead look at the LP unit valuations themselves. A common metric when looking at LP unit prices is yield: LP distribution ÷ LP price.

This metric is akin to the common dividend discount model: p = d1 ÷ (r-g). Yield = r-g.

However, there are a lot of assumptions that go into both “r” and “g.” The discount rate, “r,” represents expectations of variability or risk of the cash flows related to the business. From a risk standpoint, the nature of the MLP’s business is relevant. MLP businesses and their operational risks range significantly, from a Federal Energy Regulatory Commission-regulated interstate pipeline, to a fee-based terminal operation, to a frack sand operation, to offshore drilling rigs.

In addition, because the discount rate relates to the LP distributions, the discount rate represents a levered return. Because this levered discount rate is for the LP interest only, the level of debt is relevant, as well as the relationship with the GP interest based on the relevant current and expected IDR tier. But, more on this later.

Growth in LP distributions, “g,” is also complicated. Some MLPs are better positioned for growth in total distributions—whether through a pipeline of dropdowns from a GP sponsor or through organic growth projects. How that growth translates to LP distribution growth depends on where the MLP is in its IDR tiers—it’s harder for an MLP deep in the 50% splits to grow LP distributions than it is for a new MLP currently at the MQD level.

While there are many factors that go into yield that make it difficult to organically derive “r” and “g” to get yield, this methodology is particularly useful in comparing MLPs’ yields.

It’s easier to say MLP A is in a riskier business than MLP B and therefore should trade at a higher yield, or MLP A has a higher LP distribution growth expectation than MLP B and therefore should trade at a lower yield. Based on intuitive judgements about risk and growth, LP distribution yields can be compared among MLPs quite simply. This is probably why research analysts often use yield as their go-to valuation technique.

In the context of asset M&A or GP-LP simplifications, however, yield falls subject to the same issues in terms of relative GP-LP values described above.

So where does that leave us when trying to figure out where the actual LP-GP valuation split falls within the hypothetical band described above? We can look at actual examples to gain some insight.

Recent transactions

MLP GP-LP simplification transactions seem to be accelerating. Kinder Morgan began the trend when it rolled the MLP into the corporate sponsor, KMI. Since then, several GP-LP transactions have taken place to adjust or eliminate the IDRs, especially for MLPs where the IDRs were well into the high splits. Let’s look at two recent transactions, Williams and ONEOK, to see what conclusions can be drawn regarding the GP-LP relative valuation.

On Jan. 9, The Williams Cos. Inc. (WMB) and Williams Partners LP (WPZ) announced plans whereby WMB permanently waived its IDRs in exchange for 289 million common units of WPZ. This brought WMB’s total interest in WPZ to 72.3%. WMB effectively traded its GP interest for $11.1 billion worth of WPZ LP common units.

We know that at the time of the announcement, WPZ had been paying quarterly distributions of 85 cents per quarter for the past two years, putting WPZ well into the 50% IDR splits. The GP’s average share of distributions at the 85 cents per unit level worked out to 31%.

As discussed above, the hypothetical band of the GP’s share of equity value in WPZ would have therefore been 31%-50%. We can calculate the actual average percentage because both WMB and WPZ were publicly traded.

Prior to the announcement of the transaction, WMB owned 370.9 million WPZ units (including Class B) that were worth $14.2 billion—assuming the 10-day volume weighted average price (VWAP) prior to announcement. At that time, WMB’s equity market value was $23.7 billion and WMB had $4.9 billion of net debt (excluding WPZ debt). Therefore, at the time of announcement, WMB’s enterprise value was $28.6 billion. Subtracting the $14.2 billion value of its WPZ LP units leaves $14.4 billion of implied WPZ GP value at WMB. The market value of WPZ’s LP units at that time was $23.9 billion.

Therefore, $14.4 billion implied GP value represented 37.5% of the total WPZ “equity” value (LP and GP) implied by the WPZ and WMB trading prices at that time, or about 6.5% above the floor indicated by current WPZ distributions.

On Feb. 1, ONEOK announced a plan to simplify its structure. However, unlike Williams, ONEOK Inc. (OKE) announced its intention to exchange OKE shares for all ONEOK Partners LP (OKS) units not already owned by OKE, effectively eliminating the IDR structure.

Prior to the announcement, OKS’s quarterly distribution was $0.79, putting it well into the 50% IDR splits. The GP’s share of OKS’s total distributions (average) was 32.2%.

Like WMB, we can look at OKE’s trading metrics prior to the announcement to get an implied value of the GP interest. OKE shares’ 10-day VWAP prior to the announcement was $55.51 and there were 210.7 million shares outstanding, implying an equity market value for OKE of $11.7 billion. Adding net debt (excluding OKS debt) of $1.4 billion implied $13.1 billion of enterprise value. Subtracting the market value of the 114.3 million OKS LP units (including Class B) held by OKE of $5 billion leaves an implied value of OKS’s GP of $8.1 billion.

The $8.1 billion of GP value plus $12.5 billion of LP market capitalization prior to announcement implies that the market was effectively valuing OKS’s GP as 39.2% of OKS’s “equity” value, or 7% above the “floor” represented by the current split.

Interestingly, prior to each announcement, the market was effectively allocating equity to each GP at the same 21-22% premium to the percentage implied by the then current GP share of distributions. Of course, OKS–OKE and WPZ–WMB had very similar IDR profiles at the time of announcement.

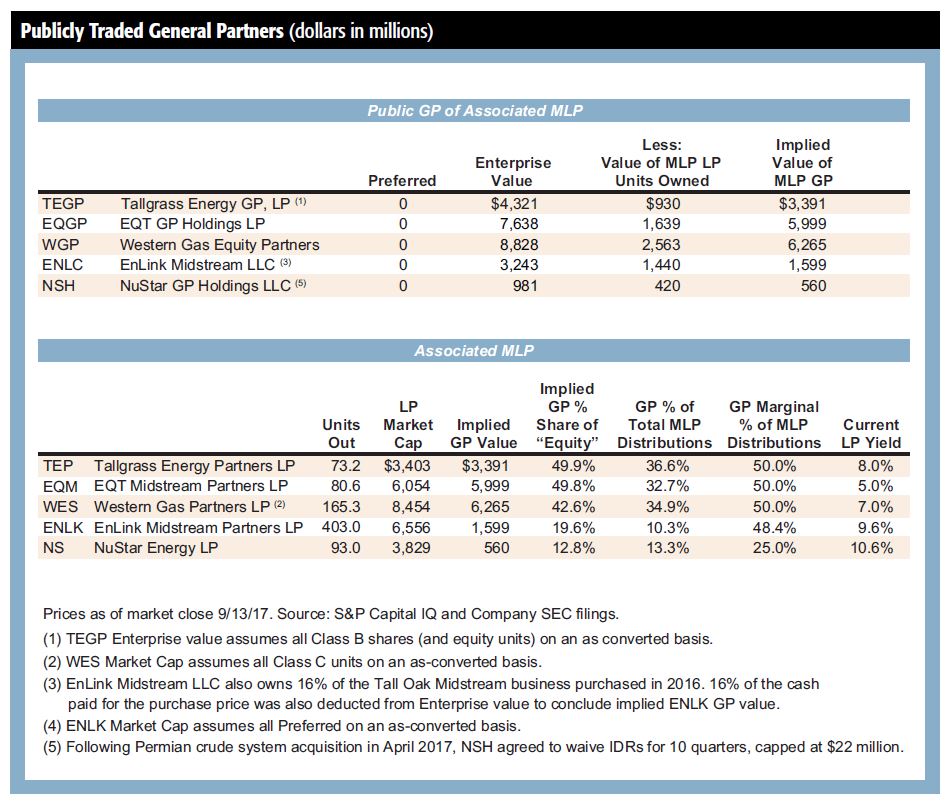
Publicly traded GPs

In addition to the data that is available regarding relative GP-LP valuations from recently announced transactions, we can look at the trading metrics of several other MLPs and their pure-play publicly traded GPs—pure-play in that the entity only owns MLP LP units and the GP interest including IDRs. In a similar manner as Williams and ONEOK, we can look at the implied enterprise value of the GP entities and then back out the value of the MLP LP units owned to get the implied value of the GP.

This can then be compared to the public market value of the LP interest in the MLP to get the implied GP share of the total “equity” in each MLP. The accompanying table shows five GP-MLP pairs ranked by implied GP percent ownership.

Option analogy

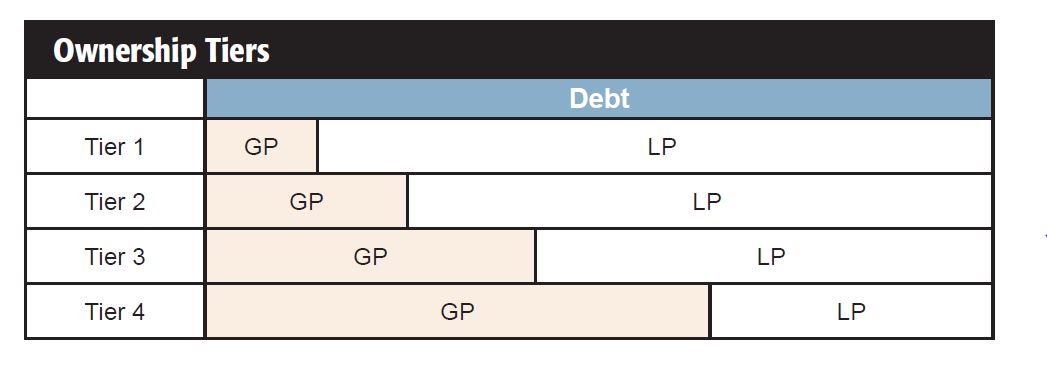
One alternative to trying to allocate equity value among the GP and LP is to consider each IDR tier as a separate security.

For example, using the hypothetical example MLP above, the enterprise value can be broken up into tiers. We know that the debt securities have a $1,000 face value. Assume a 5% coupon. Each quarter, note-holders get $12.50. Beyond that, cash flow first goes to pay the distributions up through Tier 1, Tier 2 and so forth. We know that the cash required for a full Tier 1 distribution is $41.07 (($0.4025 x 100 LP units) ÷ .98). The cash flow required for a full Tier 2 distribution is $4.106 (($0.4375 - $0.4025) x 100 LP units ÷ .85). The cash required for a full Tier 3 distribution is $11.667 (($0.5250 - $0.4375) x 100 LP units ÷ .75). Above that, cash is split 50-50.

Instead of thinking about the LP interest as a security and the GP interest as a security, think about each tier as a security with 100 “shares” that are owned by different owners. For example, the LP owns 98 shares of the Tier 1 security and the GP owns two shares; the LP owns 85 shares of the Tier 2 security and the GP owns 15 shares; the LP owns 75 shares of the Tier 3 security and the GP owns 25 shares; and each of the LP and GP own 50 shares of the Tier 4 security.

The LP trading value of each unit therefore represents 0.98 shares of Tier 1, 0.85 shares of Tier 2, 0.75 shares of Tier 3 and 0.5 shares of Tier 4.

Given that most but not all MLPs generate revenue from relatively consistent, contractual obligations and maintain some level of distribution “cushion” (i.e., they distribute less than 100% of cash flow available), few MLPs have had to significantly curtail Tier 1-3 distributions once they are in the top tier. Accordingly, for MLPs that are comfortably within the 50% splits, we can think of the Tier 1, 2 and 3 securities as similar to debt securities and then get an implied value of the Tier 4 that can be compared among MLPs.

In practice, companies utilize a contingent claims analysis based on option pricing to allocate value among the tiers, which can then be easily and mathematically allocated among the LP and GP.

While there are many ways to look at the relative valuation of an MLP’s GP and LP, from simple to complex, it is important to be aware of the dynamics when evaluating MLP transactions.

Jim Hanson is a managing director with Duff & Phelps.

Comments