E&P Exploration: Planning the Most Productive Well Path

The significant capital investment of constructing a well, in combination with the upfront uncertainty on its performance, creates one of the most difficult choice sets for profitable extraction from hydrocarbon reservoirs. A fundamental component is planning the well trajectory. Currently, well trajectories are planned with isolated, manual processes and numerous revisions involving geo- scientists, geomechanics specialists, drilling engineers and asset managers. The planning process can take days, weeks or months, but even then, the truly optimal well might not be identified because not all possible well trajectories can be evaluated by humans in a reasonable time.

A multidisciplinary team at Baker Hughes conceived and implemented an integrated method of finding the optimal wellbore path in a given reservoir. The technology considers distributed reservoir properties (e.g., porosity, permeability and saturation), satisfies constraints (e.g., pipe bend curvature limits, wellbore stability considerations and anti-collision assurance) and avoids obstructions and no-go zones within the reservoir. A Monte-Carlo approach is implemented to help cover parameter space and enforce constraints while generating ensembles of valid candidate well trajectories. The selection of the optimal wellbore path can be posed as a constrained optimization problem and solved with a novel methodology.

By starting at either the wellhead or a particular survey location along an existing well, multiple possible well path trajectories are created automatically. As each path is progressively constructed, drilling constraints, wellbore stability constraints and anti-collision constraints are enforced. Each successfully created wellbore path is scored with an objective function based on reservoir properties, for example, the length of the well exposed to reservoir rock that exceeds thresholds on porosity, permeability and hydrocarbon content.

Planning for simple and complex reservoirs

The Baker Hughes team applied this technology to several different reservoir types. Figure 1 shows a top view of a thin, heterogeneous reservoir with a distinct northwest-southeast strike of partially fragmented hydrocarbon sections. The reservoir landing location had been predetermined; it is located at the bottom mid-point of the displayed reservoir section. Also shown is an ensemble of evaluated well trajectories, all of which satisfy the drillability constraint (build-rate less than 3 degrees per 100 ft). All well trajectories were scored with the objective function, and the resulting scores have been normalized so that a score of one denotes the most productive wellbore trajectory and a score of zero denotes the least productive wellbore. Visual inspection confirms that the low-scoring well trajectories are, on average, shorter and traverse through lower-porosity reservoir rock. In contrast, high-scoring well trajectories are, on average, longer and traverse through the fragments of high-porosity reservoir rock.

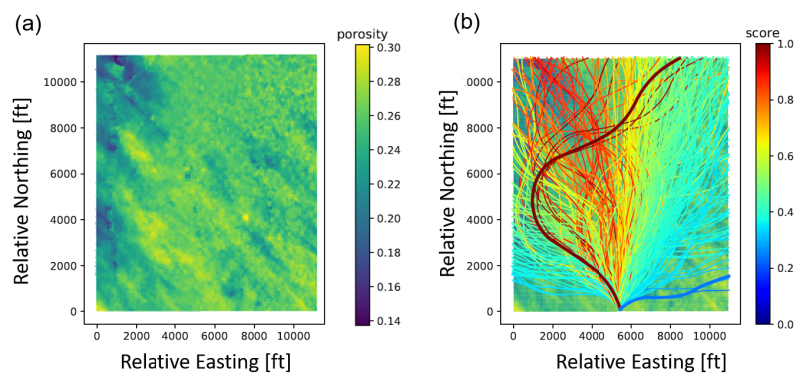
The second example reproduced here is a complex, faulted reservoir shown in Figure 2 in conjunction with the optimal well trajectory from a predetermined, fixed wellhead location. The optimal well trajectory intersects multiple faults at near-perpendicular angles and traverses through the high-productivity zones located in the eastern portion of the reservoir segment. This well trajectory avoids crossing a number of smaller faults in the east of the reservoir section, which could cause unnecessary drilling risk. However, it is worth noting that the applied technology can be adapted to include fault-avoidance constraints or penalties associated with fault-proximity or fault-crossing.

No constraint on constraints

The nature of the solution approach provides several attractive features. No matter how many candidate well trajectories are evaluated or how much compute time can be allocated, this approach always returns a best well trajectory. In a strict mathematical sense, the returned solution is not the best, because there is no guarantee of identifying the global extremum. Instead, the returned solution can be considered an approximation that, in the limit of infinite candidate wells, is equivalent to the optimum. In practice, a few thousand candidate wells, which can be generated in a time frame of minutes, already cover the spatial extent of most reservoirs in adequate detail. Subsequent candidate wells oftentimes only marginally improve the solution.

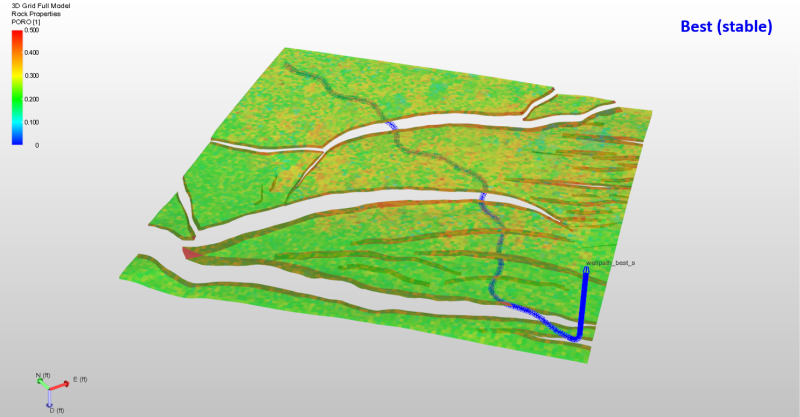
Another advantage of this approach is near-perfect numerical scalability. Because each candidate well trajectory is generally independent of each other, this methodology can easily be scaled up to any number of independent processes, each of which generates and evaluates its own sub-ensemble of candidate well trajectories. In ideal map-reduce fashion, only the resulting best well trajectories from each process will be compared to each other to determine the overall best well trajectory.

The initial implementation was focused on drillability, wellbore stability and anti-collision constraints. The approach is extremely flexible and other constraints such as fault-avoidance, cost metrics or bottomhole assembly specifications can be implemented in a straightforward manner. Furthermore, fieldwide wellbore stability constraints can be converted into an effective azimuthal window for allowable well trajectory segments. Alternatively, it is straightforward to evaluate multiple failure criteria for wellbore stability calculations at each trial well trajectory segment. Additionally, this methodology can be extended to propose the optimal well trajectory for multiple wells.

Optimum objective

Determining the optimal wellbore trajectory in heterogeneous reservoirs is a difficult undertaking, which only becomes more challenging with increasing reservoir complexity, for example, due to isolated pockets of high-value target regions within a reservoir, structural complexity or the existence of faults.

Fortunately, the problem of finding the optimal wellbore trajectory can be posed as a constrained optimization problem, for which different solution strategies exist. In this context, a solution is defined as a well- bore trajectory for which an objective function is maximized or minimized, while at the same certain constraints are satisfied.

In the initial implementation, the optimum is determined by selecting an objective function that is very quick to compute because it does not rely on full reservoir simulations. This approach thereby provides a rapid screening tool that can be followed by detailed reservoir simulations if desired. Therefore, determining an optimal wellbore trajectory is a relatively quick process, which itself can be used as an inner process within the larger iterative process or as a component in a layered solution approach. For instance, identifying the optimal well trajectory can be a component of full field development planning, during which multiple wells or multiple well pads are considered, possibly over a decadal time span. Also, multiple injector and producer well trajectories can be optimized in response to existing and evolving reservoir conditions. In unconventional scenarios, well trajectory planning can be closely coupled to well completion configurations and hydraulic stimulation scenarios. In real-time drilling or autonomous drilling applications, the optimum well trajectory can be adjusted on the fly as live data indicate a deviation from the original plan is warranted.

In general, an objective function can be of technical or economic nature. Technical objective functions include integrated permeability, exposure to hydrocarbons, producibility or likelihood of production volume. Economic metrics can include minimizing capital costs associated with drilling and completion, maximizing revenue from production, maximizing profit or net present value or even maximizing the return of investment over a specified period.

Acknowledgment:

This article is based on the OTC-30567-MS paper, “You Can Plan the Most Productive Well Path and Drill It, Too.”