Determining Dynamic Biot’s Coefficient For Unconventionals

Knowledge of the effective stress field plays a vital role in many subsurface engineering applications for unconventional reservoirs, ranging from drilling to hydraulic fracturing. A key step in estimating accurate effective stress for such applications is the calculation of Biot’s coefficient, a parameter that often is overlooked. Recent developments in rock physics can be of benefit for finding better ways to make this calculation and to improve subsurface models to achieve better engineering outcomes.

The actual behavior of wave propagation can be modeled more accurately if the subsurface is assumed to be a solid (or matrix) interpenetrated with a continuous network of pores (or voids) filled with viscous fluid and/or gas. This theory, known as poroelastic theory, has very broad applications in geomechanics and geophysics. It expresses that stress exposure of the porous rock will result in matrix deformation and volumetric changes in the pore spaces. In its exact form, pore pressure is multiplied with the Biot-Willis coefficient, which is defined as the ratio of pore volume changes to bulk volume changes at constant pore pressure (dry or drained conditions). It ranges between 0 (solid rock without pores) and 1 (extremely compliant porous solid) and can be measured either as a static or dynamic value. The traditional method of measuring Biot’s coefficient is referred to as “static Biot,” which uses a drained triaxial compression measurement under a constant volumetric strain condition in a laboratory. This approach is expensive, time-consuming and very dependent on core availability and intervals with good core retrieval. A more practical and affordable method uses sonic log data to calculate dynamic Biot’s coefficient through the equation α= 1-K_dry/K₀ (1) where K_dry and K₀ are dry rock and effective mineral modulus, respectively.

The method that uses sonic well logs is very convenient but heavily dependent on the quality of sonic measurements and K_dry calculation. Rock physics modeling is a highly effective tool in this regard for improving the calculation of dynamic Biot’s coefficient from sonic logs by removing possible errors in sonic data and providing a better estimation for K_dry and K_dry/K₀. An appropriate rock physics template that is defined on a crossplot between K_dry/K₀ and porosity is normally recommended for the calculation of Biot’s coefficient.

Joint petrophysics and rock physics study

A study with high-quality acoustic and density logs from multiple wells was conducted to demonstrate the value of linking petrophysics and rock physics to determine dynamic Biot’s coefficient. One important input needed for this kind of study was a detailed interpretation of the rock. This was modeled using a generic stochastic method in GeoSoftware’s PowerLog petrophysical interpretation software. Seismic petrophysics also was performed in RPM, its rock physics add-on module, with direct links to other PowerLog modules.

The high-quality well log data for this study came from three wells in the Barnett Field underlying the suburbs of Dallas. The reservoir interval is the Barnett Formation, the first unconventional reservoir to be discovered in the U.S. and one of the country’s most famous producing formations. The available well log data put through a seismic petrophysics workflow determine reservoir properties. The proposed workflow starts by examining the well log data, calculating the elastic properties of the rocks and checking the quality of the saturated bulk and shear modulus. The volume of clay is then determined and a lithological model of the reservoir is generated accordingly. This lithological model is used to build a rock physics model, and then Poisson’s ratio, Young’s modulus, K_dry and Biot’s coefficient are calculated. The lithological description of the formation is created using stochastic methods in PowerLog, and then the mineral volumes are used to compute K₀ using the Voigt-Reuss-Hill average method. A rock physics workflow is then developed in RPM to determine elastic rock properties. Next, K_dry is calculated using three different methods: using measured sonics and density with Gassmann, a rigorous computation using differential equation medium (DEM) theory, and a rock physics modeling strategy that assumes saturated and dry bulk modulus values are very similar to each other. This assumption is acceptable because in unconventional reservoirs porosity is very low and fluid effects are minimal. In the third method, Ksat is calculated using modeled density and sonic velocities and then used instead of K_dry in equation (1) to calculate Biot’s coefficient.

Figure 1 compares the results for these three methods for K_dry calculation. The results show that the assumption made in the rock physics modeling method (the third approach) is validated by the results for these wells, which show less scattered data with the same trend in comparison to the other two scenarios.

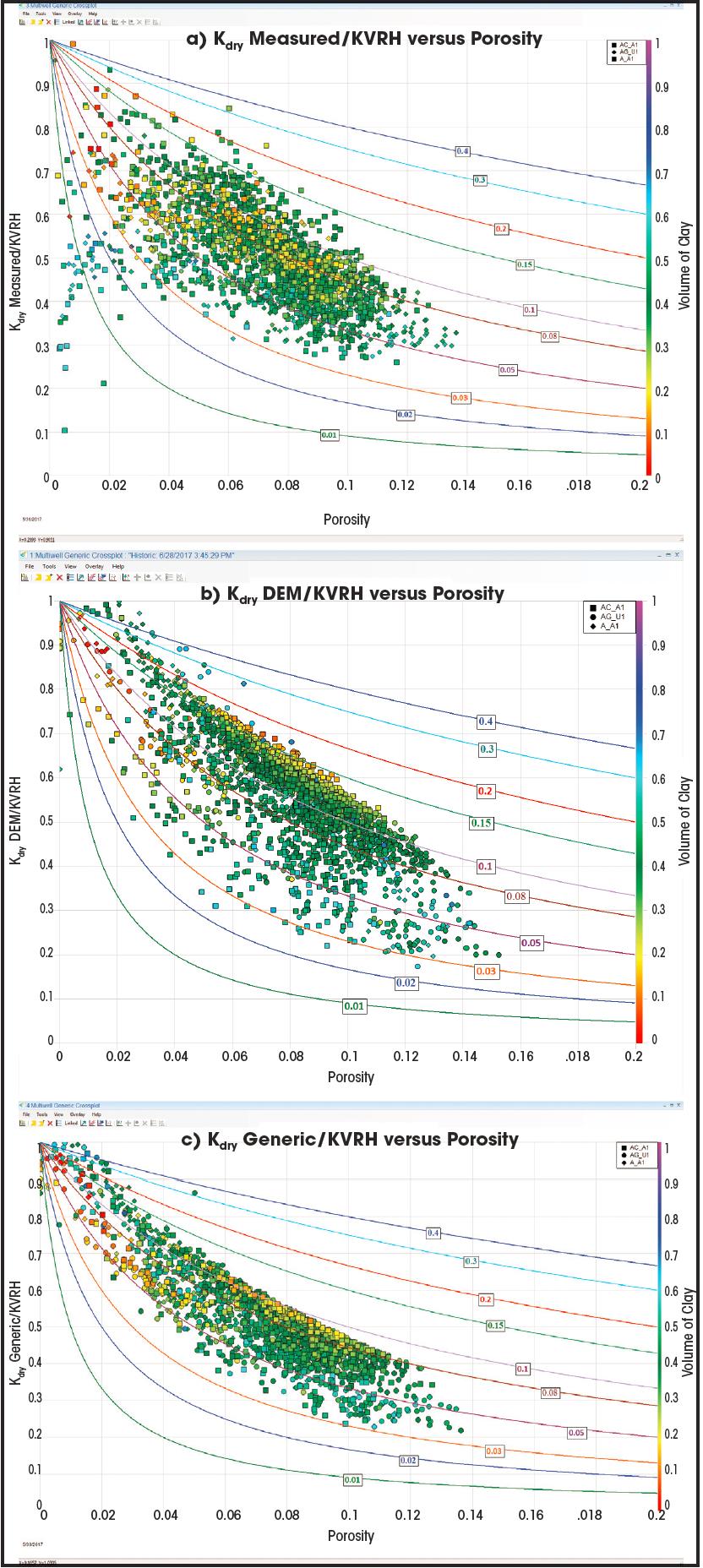
FIGURE 1. K_dry/K₀ is compared to porosity cross-plots using three different approaches for calculating Kdry: a) using measured sonic and density logs with Gassmann, b) using DEM rock physics and c) using a rock physics modeling of logs and assuming that the K_dry value is similar to the Ksat value. The rock physics template for Biot’s coefficient is overlaid on the cross-plots. (Source: CGG)

This calculated K_dry is used in combination with K₀ to determine the vertical dynamic Biot’s coefficient. In addition, both measured and synthetic data are used to analyze the elastic properties and physical characteristics of the given formation.

Figure 2 shows this analysis by generating a dynamic Biot’s coefficient curve calculated using the rock physics modeling approach and using the measured logs. The rock physics modeling approach preserves the measured trend with very similar results (less data scattering that potentially could come from different noise sources). The dynamic Biot’s coefficient method incorporates the information assembled from analysis of measured logs to generate synthetics, which can then be used with seismic to generate a subsurface cube for dynamic Biot’s coefficient for geomechanical and engineering applications such as pore pressure prediction, wellbore stability, depletion effects, reservoir integrity and geomechanical simulations.

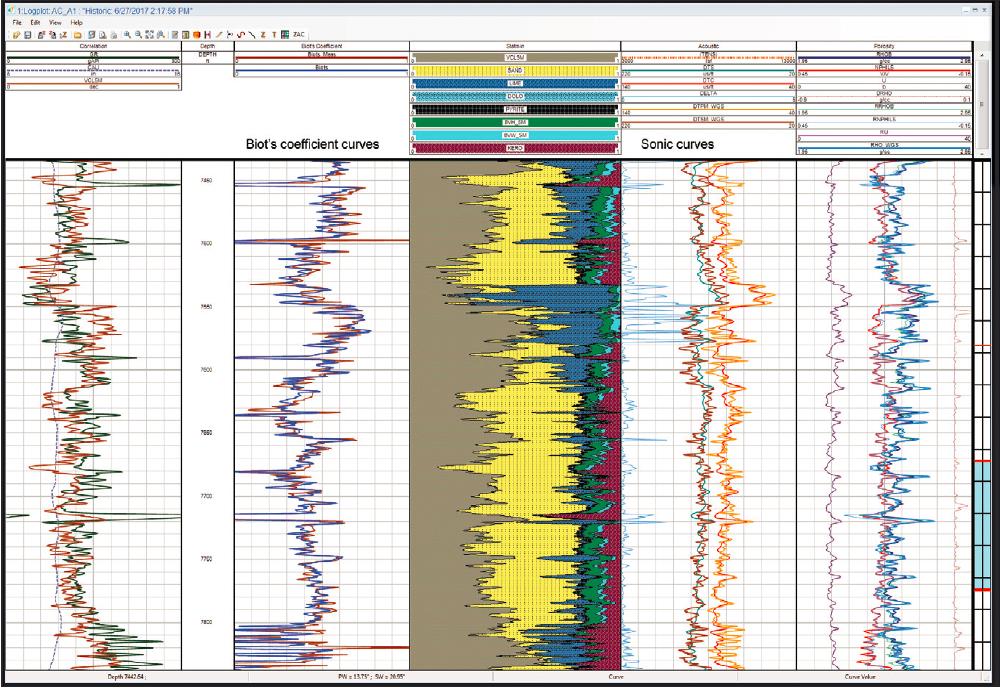
FIGURE 2. The calculation of dynamic Biot’s coefficient curve (second track from left) along one of the wells using the measured logs (red) and the third method based on rock physics modeling (blue) are displayed. (Source: CGG)

The presented rock physics modeling strategy can help to better estimate Biot’s coefficient using well log data. Such physics-based strategy will address possible errors in the interpreted logs and prepare them for a better match with seismic. This will improve the match between 1-D synthetics (derived from elastic logs) and measured seismic, resulting in a more accurate 3-D attribute volume for dynamic Biot’s coefficient.

This study illustrated how the integrated usage of petrophysical tools of PowerLog and rock physics modeling in RPM can improve interpreted logs through a seismic petrophysics workflow. Furthermore, the obtained results can be used with a seismic dataset to generate a cube of Biot’s coefficient for use in 3-D geomechanical studies for drilling and completion design.

References available.

Contact Rhonda Duey at rduey@hartenergy.com for more information.